Timewalk Correction

Timewalk is a phenomenon observed in pixel detectors, such as the Timepix3 detector, where events with higher energy appear to arrive earlier than events with lower energy. This occurs because the Time Over Threshold (ToT) of a signal is inversely related to its time of arrival (ToA). A constant threshold is set, and signals with larger ToT have a steeper gradient, leading to a perceived earlier arrival time (see fig-timewalk-effect-thresholding). This phenomenon is known as timewalk.

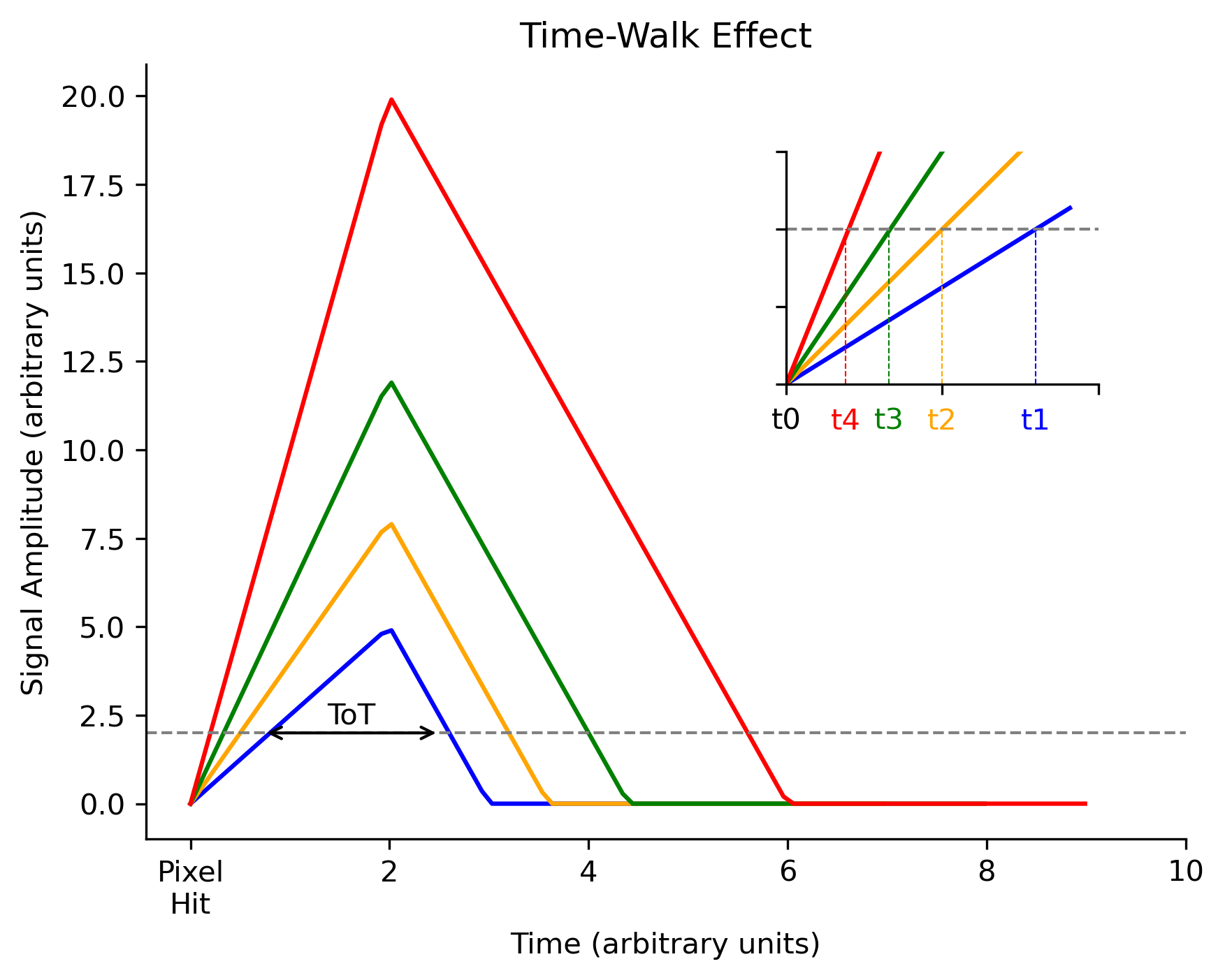
Figure 1: Illustration of the timewalk effect, where signals with higher ToT values appear to arrive earlier than those with lower ToT values, despite actually occurring simultaneously. All events arrive at p0 and yet the moment at which the signal crosses the threshold is earlier for signals with larger energy (higher peak, steeper curve).

In experimental setups, a more precise correction for timewalk is typically achieved using test pulses to circumvent the discriminator (constant threshold) and get a true ToA. Then at a known (but short) time interval later the pixel matrix is stimulated. This process is repeated with varying energies to accumulate data that can inform a calibration curve which is then used to provide a correction factor, which is subtracted from the ToA. Readers are referred to Pitters et al. (2019) (DOI: 10.1088/1748-0221/14/05/P05022) for a more detailed discussion on experimental pixel by pixel timewalk correction. However, this method requires detailed experimental setup and calibration.

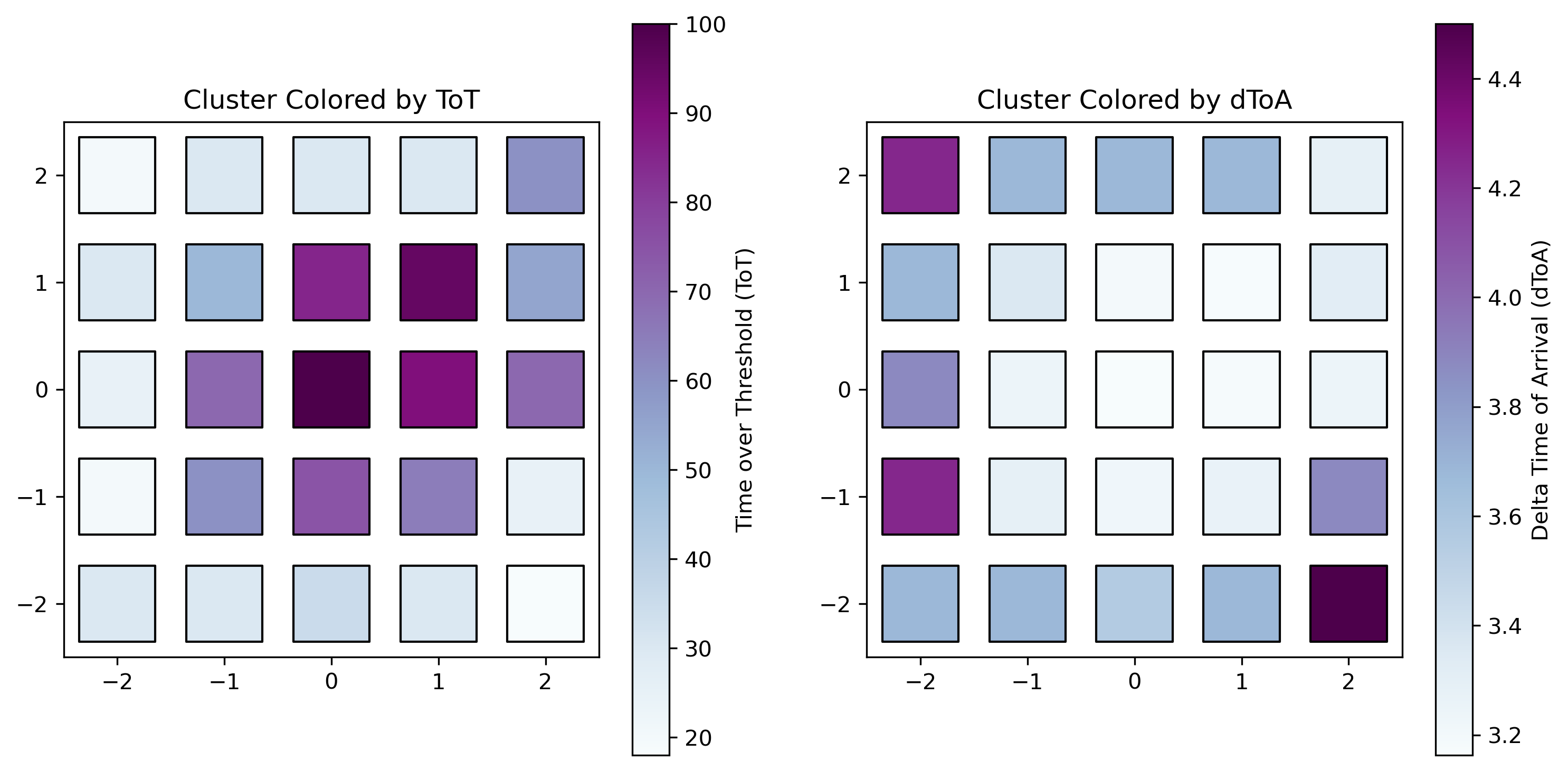
Figure 2: Heatmaps showing the the timewalk effect within a single cluster. Where the Time over Threshold (ToT) is large the dToA is small and vice versa.

Luna offers an alternative, statistical method for correcting timewalk effects without the need for such detailed experimental calibration. Instead of using test pulses, Luna estimates the “true” time of arrival (ToA) using cluster data, which provides an approximation of true ToA (fig-timewalk-effect-within-cluster). Although this statistical method is less precise than the experimental approach and does not correct for pixel-by-pixel variations—opting instead to average these variations across pixels—it still offers a significant improvement in accuracy compared to the uncorrected ToA. Over large enough sample sizes, the statistical method is expected to converge towards greater accuracy.

Timewalk Correction in Luna

Luna’s approach to correcting timewalk is based on a statistical method that utilizes cluster data instead of test pulses to estimate the true time of arrival. The algorithm can be described through the following steps, both in words and using mathematical notation:

1. Cluster Time of Arrival (cToA) Estimation:

   The time of arrival for a cluster (cToA) is estimated as the time of arrival of the pixel with the maximum energy (cToT) within the cluster.

   \[t_{\text{cToA}} = t_{\text{ToA}}( \text{argmax}( \text{ToT}))\]

   where

   \[t_{\text{ToA}}( \text{argmax}( \text{ToT}))\]

   represents the time of arrival of the pixel with the maximum ToT within the cluster.

2. Delta Time of Arrival (dToA) Calculation:

   For each pixel in the cluster, the Delta (difference in) Time of Arrival (dToA) is calculated relative to the cToA. This is expressed as:

   \[\Delta t_{\text{dToA}} = t_{\text{ToA}} - t_{\text{cToA}}\]

3. Timewalk Matrix Construction:

   The dToAs are grouped into a two-dimensional matrix based on their ToT and the cluster’s cToT. This matrix, known as the Timewalk Matrix, is used to analyze the timewalk effect across different energy levels. The matrix is constructed by averaging the dToAs within each bin, defined by the pixel’s ToT and the cluster’s cToT:

   \[M(i, j) = \frac{1}{N(i, j)} \sum_{\text{hits}} \Delta t_{\text{dToA}}\]

   where

   \begin{align*} M(i, j) & = \text{is the matrix entry for ToT bin i and cToT bin j} \\ N(i, j) & = \text{is the number of hits in that bin} \end{align*}

   Note

   In luna output the Timewalk Matrix is in Long form, where each row represents a (cToT, ToT) pair. Rows which are empty (i.e. no cToT/ToT intersection) are removed before writing to disc.

4. Lookup Table Generation:

   The Timewalk Matrix is used to generate a lookup table of correction factors, which are then applied to correct the time of arrival (ToA) of pixel hits. This process involves the following steps:

   • Plotting a heatmap of the Timewalk Matrix with cluster ToT values on the X-axis and pixel ToT values on the Y-axis.

   • Determining a cToT cut by analyzing the heatmap to identify where further increases in cToT result in minimal changes to the timewalk correction.

   • Discarding data below the cToT cut, and averaging the remaining data to determine the correction factor for all cToT values higher than the cut. This correction factor, denoted as $L(j)$, is calculated by:

   \[L(j) = \frac{1}{|J|} \sum_{i \in J} M(i, j)\]

   where

   \[\begin{split}\begin{align*} L(j) &= \text{the lookup table entry for pixel ToT bin j}\\ J &= \text{the set of bins above the cToT cut} \end{align*}\end{split}\]

5. Timewalk Correction

   The correction factor $L(j)$ is then subtracted from each pixel’s time of arrival to correct for timewalk effects:

   \[t_{\text{corrected}} = t_{\text{ToA}} - L(j)\]

   Here,

   \[\begin{split}\begin{align*} t_{\text{corrected}} &= \text{the corrected time of arrival} \\ t_{\text{ToA}} &= \text{the original time of arrival}\\ L(j) &= \text{the lookup table correction factor corresponding to the pixel's ToT} \end{align*}\end{split}\]

Conclusion

Luna’s timewalk correction offers a practical and scalable method for mitigating timewalk effects in pixel detectors like the Timepix3. By using statistical analysis of cluster data, Luna provides a way to correct for timewalk without the need for extensive experimental calibration, making it suitable for a wide range of applications in high-energy physics and other fields where timewalk is a concern.

Acknowledgements

We thank Dr. Peter Svihra for sharing his method of timewalk correction with us to implement in Luna.